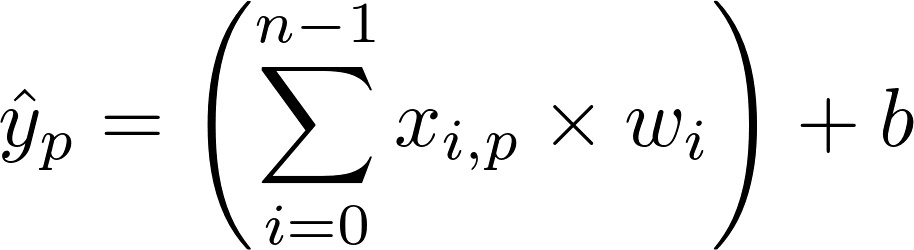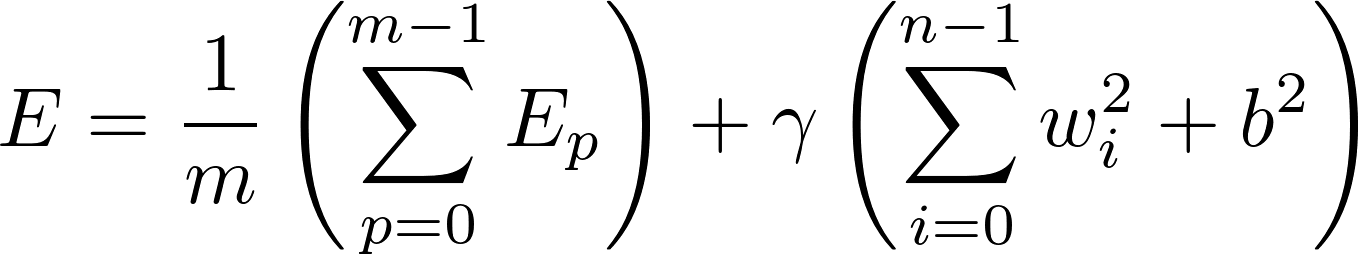CS 5043: HW1

Assignment notes:

Deadline: Friday, February 8th @11:59pm.
Hand-in procedure: submit to the HW1 dropbox on Canvas.
This work is to be done on your own. While general discussion about Python and TensorFlow is okay, sharing solution-specific code is inappropriate. Likewise, you may not download code solutions to this problem from the network.
Submit PDF and Jupyter notebook files only; do not submit zip or MSWord documents.

Linear Network

In class, we developed an implementation of gradient descent for a linear network in raw TensorFlow. The notebook that we developed was posted on Canvas. The code that we developed and the math on the board deviated in a couple of subtle ways. I have a full derivation that is consistent with the code.

For this homework, we will exercise your math, Python and TensorFlow skills. There are two parts to be done in sequence:

Augment our implementation to add a bias term to our model.
Augment our implementation to add a regularization term to the cost function.

Data Set

For the example in class, we predicted the zero'th column of the torque matrix from the neural data. For this homework, we will use the one'th column of the theta matrix. This corresponds to the position of the elbow (measured in radians).

When you load data, use the theta line rather than the torque line.
When you configure your data sets, reference the theta variable in both your training and validation output variables. Also, reference column 1 in this matrix (change [:,0] to [:,1]).

Part 1: Bias Term

Add a bias term to our linear model (this is another paramter, just like the weights):

Steps:

Add a b variable to the graph. Set the initial value to zero.
Make any changes that are necessary to the forward model.
Make any changes to gradients that are necessary.
Compute the gradient for b. Hint: tf.reduce_sum() is useful here.
Add a new training operation for b to the graph.
Run this training op in your learning loop. Remember that you can "run" multiple operations at once.

Execution:

Execute 2000 epochs of training. Your learning loop should be displaying FVAF for both the training and validation sets every 10 epochs.
Execute b.eval(). This should report a non-zero value.

Generating the report:

Save your notebook (keep a copy for your records).
Generate a PDF from your notebook (File/Export/PDF). Make sure that your PDF file includes: your code, your training run and the result of querying the final value of b.

Part 2: Regularization

Add a regularization term to the learning algorithm:

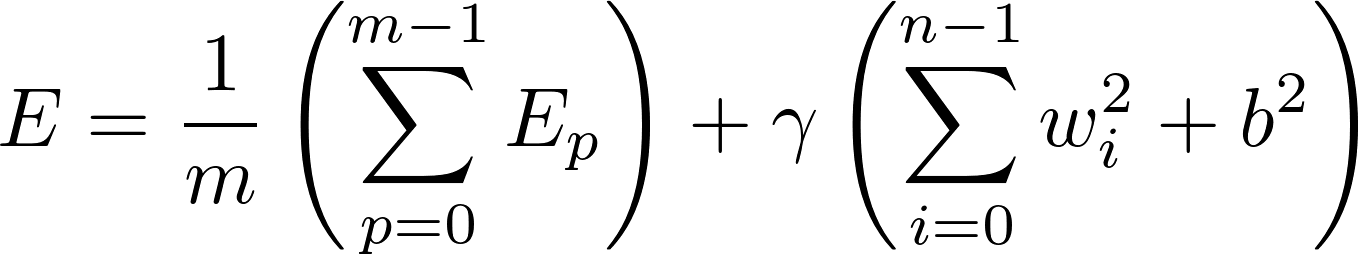
Steps:

Modify the gradients computation.
Modify the gradients_bias computation (the gradient computation for the bias term).
Select gamma = 2

Execution:

Execute 2000 epochs of training. Your learning loop should be displaying FVAF for both the training and validation sets every 10 epochs.
Execute b.eval(). This should report a non-zero value.

Generating the report:

Save your notebook (keep a copy for your records).
Generate a PDF from your notebook (File/Export/PDF). Make sure that your PDF file includes: your code, your training run and the result of querying the final value of b.

What to Hand-In

Hand in both Jupyter notebooks and the corresponding PDFs.

Notes

Once you construct your graph and start your session, the graph cannot be changed (the way that we have set things up, both alpha and gamma are fixed when you start your session). If you do need to make changes, then the prudent things to do are to 1) close the session, and 2) reset the graph. In the notebook that I provided, there is a cell toward the bottom that will do both of these things. Once you execute it, you can construct a new graph, start the new session and begin training.

andrewhfagg -- gmail.com

Last modified: Mon Feb 4 12:17:12 2019